本篇文章中，我们将从常用的切线放缩和泰勒展开出发，探讨一些在高中数学中常用的逼近与放缩方法，并简单介绍他们的应用。

2022 年新高考 I 卷中出现的比较 $a=0.1e^{0.1}$，$b=\dfrac 19$，$c=-\ln 0.9$ 三个数大小的选择题即为这种方法的典型例题。

1. 切线放缩

高中阶段有一类常用的不等式：

这些不等式都是由原式在某点的切线方程得到的，切线方程和原函数的在该点的值和一阶导都相同。通过泰勒展开，我们可以把这种思想从一阶推广到 $n$ 阶甚至任意阶。

2. 泰勒展开

对于多项式 $f(x)$，我们定义 $T_n(x)=\sum\limits_{i=0}^n\dfrac{f^{(i)}(x_0)(x-x_0)^i}{i!}$ 为其 $n$ 阶泰勒级数（Taylor Series）。$T_n(x)$ 与原函数在 $x_0$ 处有相同的 $n$ 阶导数，即对于任意 $k\in [0,n]$，$f^{(k)}(x_0) = T_n^{(k)}(x_0)$。特别地，当 $x_0=0$ 时，该级数又称作原函数的麦克劳林级数（Maclaurin Series）。

2.1.1. 应用：得到常用不等式

对一些函数进行泰勒展开，我们可以得到一些常用的不等式，如：

由 $e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\cdots$ 我们可以得到 $e^x\ge x+1,\quad e^x\ge \dfrac{x^2}{2} +x+1$ 等不等式。

类似的，由 $\ln (x+1)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\cdots$ 可以得到 $\ln(x+1)\ge x-\dfrac{x^2}2(x\ge 0)$，$\ln(x+1)\le x-\dfrac{x^2}2(x\le 0)$ 等，注意在 $0$ 的两侧不等号的方向是相反的。

简单三角函数也可通过泰勒展开得到一些常用的不等式，由 $\sin x = x-\dfrac{x^3}{6}+\dfrac{x^5}{120}+\cdots$ 可以得到 $\sin x \leq x(x\ge 0)$，$\sin x\geq x(x\le0)$，$\sin x \ge x - \dfrac {x^3}{6}(x\ge 0)$，$\sin x\ge x-\dfrac{x^3}{6}(x\le 0)$ 等。类似的，由 $\cos x = 1-\dfrac{x^2}{2}+\dfrac{x^4}{24}-\cdots$ 可以得到 $\cos x \ge 1 - \dfrac{x^2}2$ 等。

这种方法并不总能成功，我们需要另外验证不等式成立的范围。

3. 帕德逼近

帕德逼近与泰勒展开的想法类似，对于函数 $f(x)$，我们构造一个分式 $R_{n,m}(x)=\dfrac{p_n(x)}{q_m(x)}$，其中 $p_n(x),\;q_m(x)$ 分别为 $n$、$m$ 次多项式。我们需要找到这样的分式，满足在 $x_0$ 处与原函数有相同的 $n+m$ 阶导数，即对于任意 $k\in [0,n+m]$，$f^{(k)}(x_0) = R_{n,m}^{(n+m)}(x_0)$。这样的 $R_{n,m}(x)$ 就是原函数在 $x_0$ 处的 $[n,m]$ 阶帕德逼近。

常见函数的帕德逼近参见下表，可由代码 pade.py 验证。

3.1.1. 应用：一类“比大小”问题

一般的做法肯定是构造函数，但这里我们试图用 $[2,2]$ 阶帕德逼近的结果代入一下：

先比较简单的两个，发现 $a<b$ 且 $c<b$，还需要一个三位数乘四位数的乘法就可以得到答案，相比直接构造还是能省下不少时间。

下图由 Geogebra 绘制，可以发现我们的精度在 $x=0.1$ 处可谓绰绰有余。

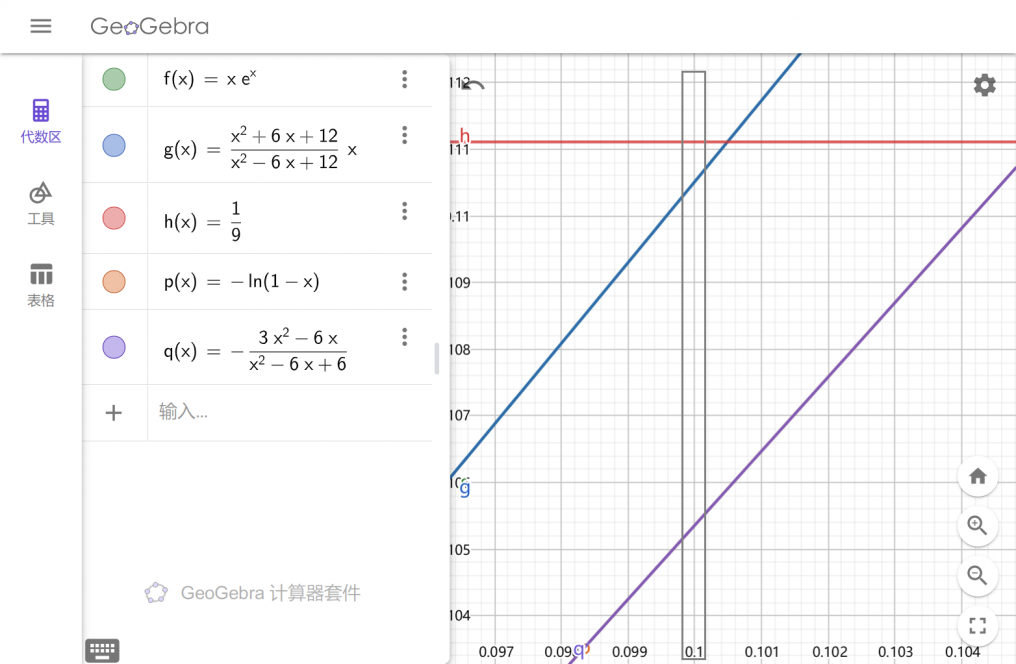
3.1.2. 应用：手算 $\ln(x)$ 的值

将 $x$ 拆分成 $x=2\cdot \dfrac{c_1+1}{c_1}\cdot \dfrac{c_2+1}{c_2}\cdot \dfrac{c_3+1}{c_3} \cdots$ 的形式，然后代入 $\ln 2=0.693$，$\ln\left(\dfrac{n+1}{n}\right)\sim\dfrac{2}{2n+1}\quad (n\ge 3)$ 得近似值。

注意到 $\ln\left(\dfrac{n+1}{n}\right)\sim\dfrac{2}{2n+1}$ 这一近似实际上就是 $\ln(x+1)$ 的 $[1,1]$ 阶帕德逼近。

这种方法一般情况下可精确到 $2$ 至 $3$ 位，$x\le 1000$ 时最大误差约为 $0.0071$（参考代码：ln-x.py）。比直接使用帕德逼近精度更高，且计算量较小，适合笔头计算。