本篇笔记概述了数字系统和信息的基本概念，包括数字电路、数字信号与模拟信号的区别，逻辑系统的分类（组合电路与时序电路），以及数字计算机和嵌入式系统的结构与设计过程。此外，还介绍了数字系统中的进制、编码方式（如 BCD 码、格雷码和奇偶校验码）等内容，帮助读者理解数字逻辑设计的基础知识。（由 gpt-4o-mini 生成摘要）

1. 数字系统 Digital Systems

1.1. 信息表达 Information Representation

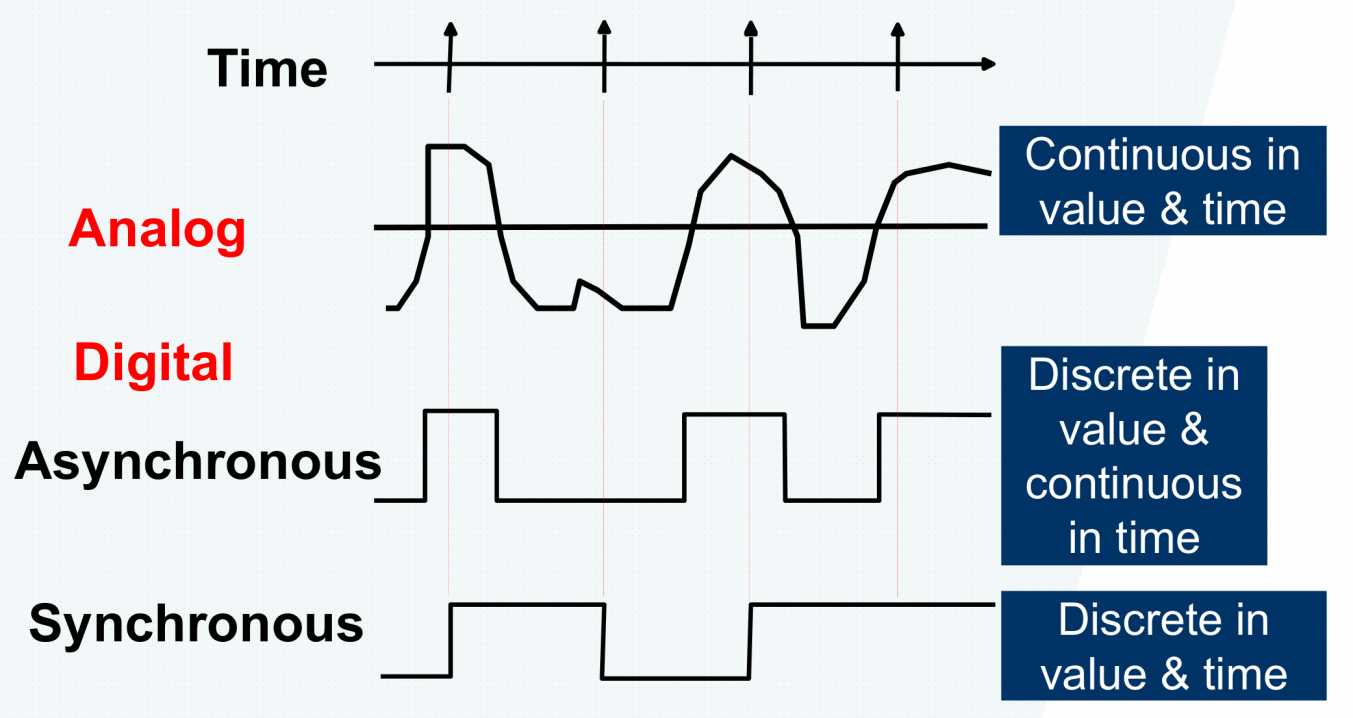
• 模拟信号(analog signal)：取值是连续(continous) 的。
• 数字信号(digital signal)：取值是离散(discrete) 的。
  • 异步(asynchronous)：在变化的时间点上是连续的。
  • 同步(synchronous)：在变化的时间点上也是离散的；由时钟脉冲控制。

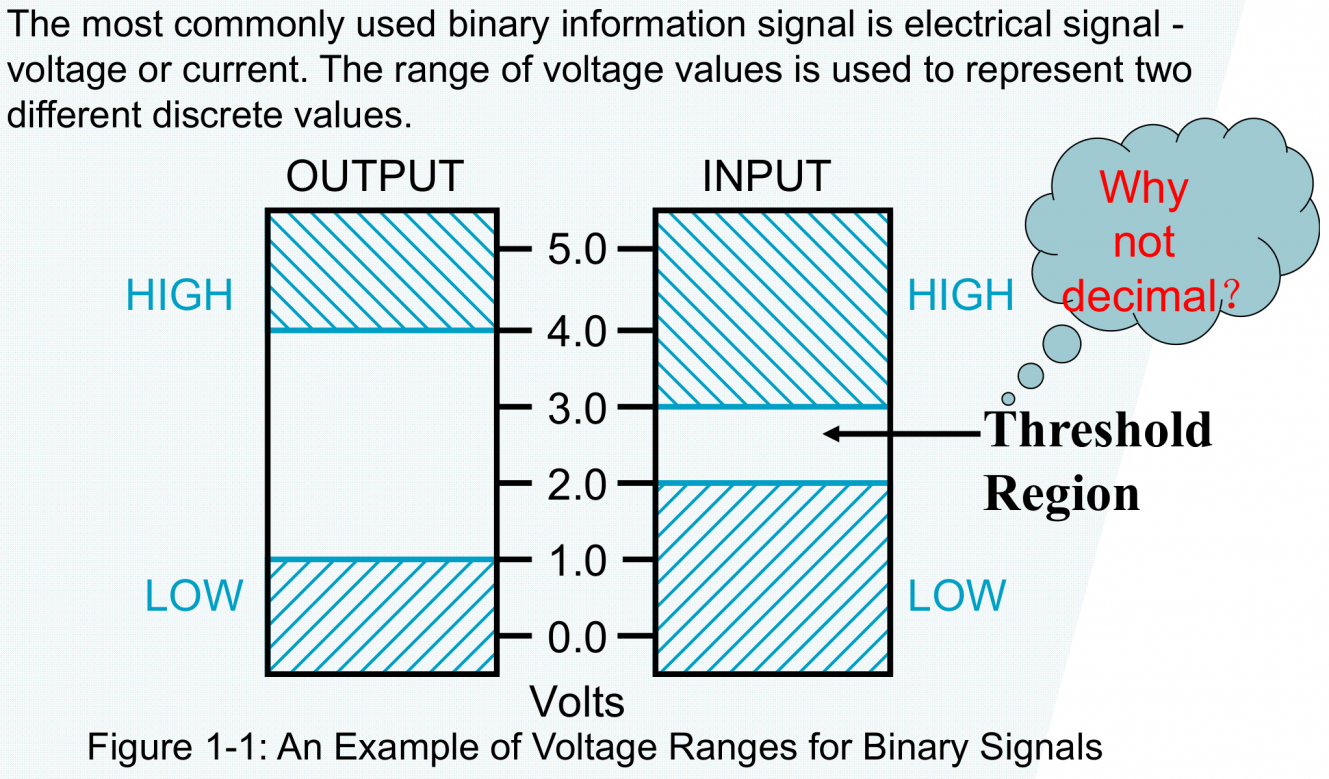
• HIGH 和 LOW 是噪声容限。
• 图中 HIGH 和 LOW 的接受范围内存在一段阈值区间，落在这一部分的电平是未定义(undefined)  的，也被称为是浮动(floating)  的。如果输出的电平是在浮动区间的，那么其认定值将是随机的。
• 硬件层面上，将模拟信号转化为数字信号的工作一般通过晶体管(transistors)  实现。

1.2. 逻辑系统 Logic System

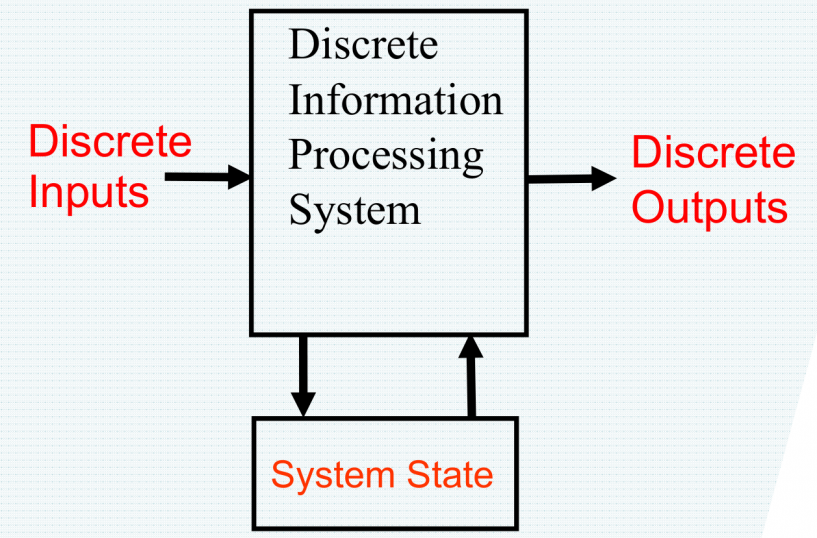
• 组合电路和时序电路的主要区别在于有没有系统状态(system state)。

1.2.1. 组合电路 Combinational Logic System

• 没有状态 No state present
• 只需要推导出一个函数即可 Output Function: Output = Function(Input)

1.2.2. 时序电路 Sequential Logic System

• 存在状态 State present
  • Synchronous Sequential System <=> State updated at discrete times
  • Asynchronous Sequential System <=> State updated at any time
• 次态方程 State Equation: Next State = Function(Current State, Input)
• 输出方程 Output Function: Output = Function(State, Input(optional))

1.3. 数字计算机 Digital Computer

数字计算机(digital computer)：A general-purpose system used to process the discrete values

嵌入式系统(embedded system)：Computers as integral parts of other products

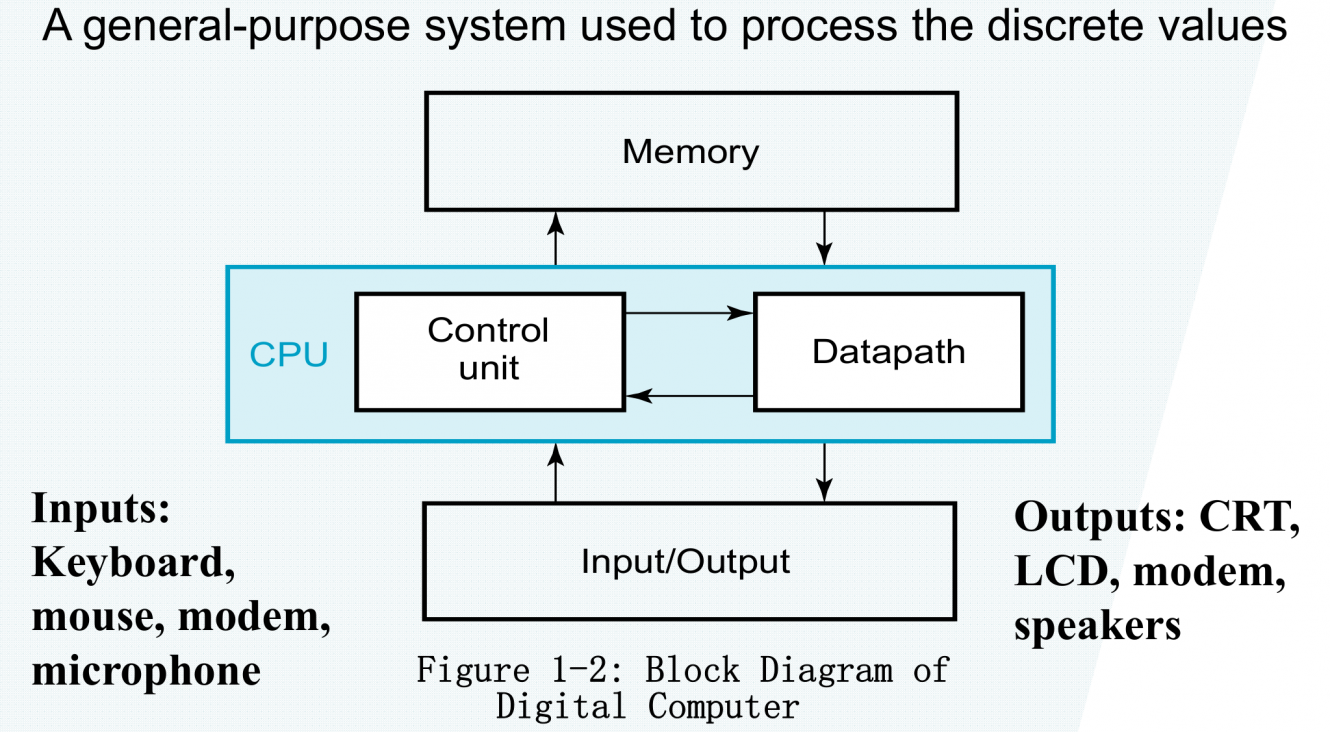
• 是典型的 Synchronous Sequential System。

1.3.1. 计算机系统结构

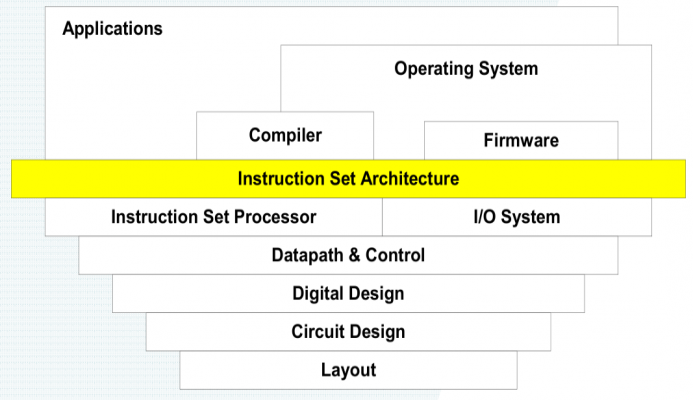
• Algorithm
• Programming Language
• Operation System
• 指令集结构 Instruction Set Architecture (ISA)
• Microarchitecture
• Register Transfer
• Logic Circuit
• Transistor Circuit

1.3.2. 设计过程 Design Procedure

如何设计一个程序？

1. Specification
2. Formulation
3. Optimization
   • Apply 2-level and multiple-level optimization
   • Draw a logic diagram or provide a netlist for the resulting circuit using ANDs, ORs, and inverters
4. Technology Mapping
   • 用已有的原件实现功能（eg. 实现 XOR Gate
5. Verification
   • 验证结果是否正确

2. 数字系统 Number System

2.1. 进制 Base

• 进制(radix/base)：collection of numberal symbols used to represent numbers in number system
• 权重(digit weight): the counting unit value of basic digital symbols in different position. ie, weight W
• 表示(representation)：digits of a number N are listed From left to right, length n+m（有整数部分和小数部分）
  • String of Digits: $(N)_R = (A_{n-1} A_{n-2} \ldots A_1 A_0 \cdot A_{-1} A_{-2} \ldots A_{-m+1} A_{-m})_R$
  • 全展开式(Power Series): $(N)_R = \left(\displaystyle\sum_{i=-m}^{n-1} A_i R^i\right)_R$

2.2. 进制转换

略。

• 别忘了小数怎么搞。
• 舍入(rounding) 的问题。

3. 编码 Coding

3.1. 独冷码 & 独热码 One-Hot & One-Cold Code

独热码(one-hot)  要求比特向量中只有一位是  1，例如  0001，0010，0100，1000  等；对应的还有独冷码(one-cold)。

使用这种编码的好处是，决定或改变状态机目前的状态的成本相对较低，容易设计也容易检测非法行为等。

但是相对应的，缺点是信息表示率较低，非法状态非常多而有效状态很少。

3.2. BCD 码 Binary Coded Decimal Code

3.2.1. 8421 Code

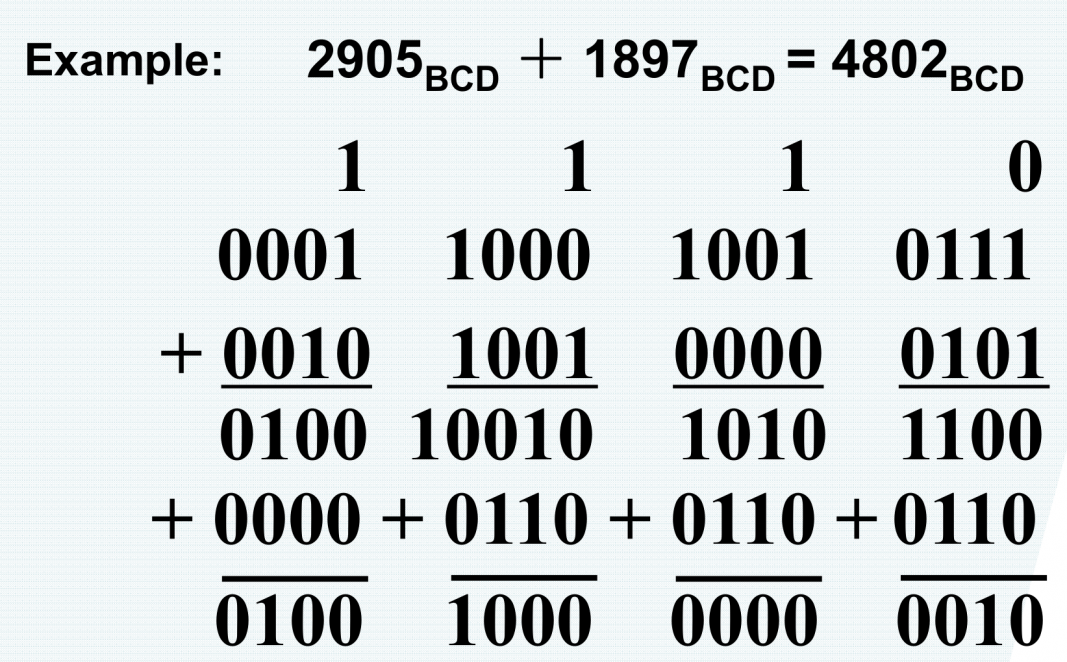
最经典的 BCD 码是 8421 码，用 4 位二进制表示一个十进制位，weight 分别为 8421，所以 BCD 码也叫做 8421 码。

• BCD 码在做加法时，类比十进制加法一样按 4 位一组计算。
• 当两位相加的结果大于 10 时需要做一个 +6 的修正。

3.2.2. Excess3 Code

余三码(Excess3) 是 BCD 码的一个改进，其核心思路是在 BCD 码的基础上，增加一个大小为 3 的偏移量。（每一位都是先 +3 再转化成二进制）

• 进位检测：注意到 $3=\dfrac{16-10}{2}$，这样十进制下能进位的两个数位，在余三码下也刚好能进位。

3.2.3. 2421 Code

2421 码与 8421 码类似，但是每一位的权值分别为 2421。$0\sim 9$ 中的每一个数都对应一个唯一的 2421 码，但将不在这一对应表中的二进制编码转换回十进制时也能对应到 $0\sim 9$ 中的数字。

• 2421 码的一个特性是 $x$ 和 $9-x$ 的 2421 码互补，其中 $x=0 \sim 4$ 时的 2421 码就是其二进制，而 $x=5\sim 9$ 的 2421 码就是 $9-x$ 与 $1111_{(2)}$ 异或后的结果。

3.3. 格雷码 Gray Code

格雷码(gray code) 是一种可靠性编码(reliable code)。相邻的两个数字的格雷码只有一个 bit 上的 0/1 不同。

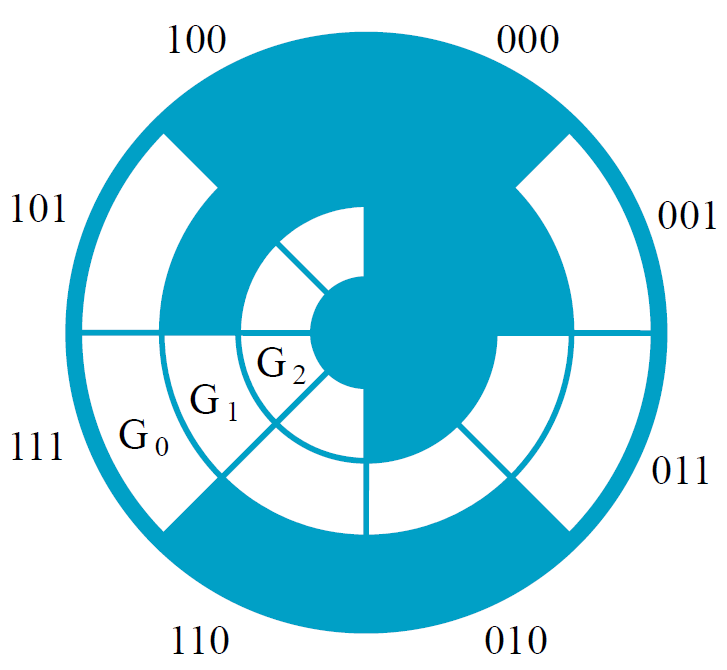从光学透镜的角度理解格雷码

3.4. 奇偶校验码 Parity Code

奇偶校验码(parity code) 也是一种可靠性编码，分为偶校验码和奇校验码两种。偶校验码(even parity code) 保证数据中为 1 的 bit 数为偶数，奇校验码(odd parity code) 保证为奇数。

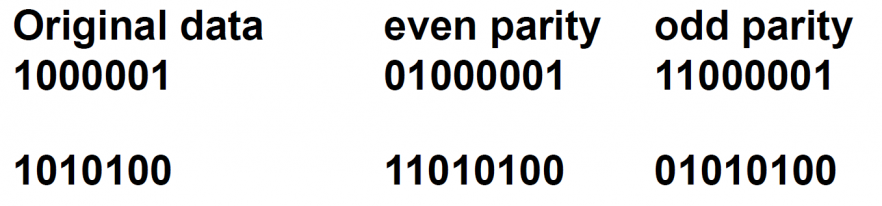奇偶校验码示例

• 需要注意是奇校验还是偶校验
• 需要注意是补在最高位还是最低位