Ch3 Algorithm

本篇笔记主要介绍了算法的基本概念，包括算法的定义、性质、函数的增长以及算法的复杂度等内容。通过对这些内容的深入探讨，读者将能够理解算法在计算机科学中的重要性，并掌握评估和分析算法性能的基本方法。（由 gpt-4o-mini 生成摘要）

1. 算法 Algorithms

1.1. 导论 Introduction

An 算法(algorithm) is a finite set of precise instructions for performing a computation or for solving a problem.

1.2. 算法的性质 Properties of Algorithms

算法一般都有一些共同性质，在描述与评价算法时这种性质是常用的。

输入(input)：An algorithm has input values from a specified set.
输出(output)：From each set of input values, an algorithm produces output values from a specified set.
确定性(definiteness)：算法的每一步都应该被精确定义。The steps of an algorithm must be defined precisely.
正确性(correctness)：算法应该给出正确的输出结果。An algorithm should produce the correct output values for each set of input values.
有限性(finiteness)：算法应当在有限步内结束。An algorithm should produce the desired output after a finite number of steps for any input in the set.
有效性(effectiveness)：算法的每一步都可以被有效执行。Each step of an algorithm must be executed exactly and in a finite amount of time.
通用性(generality)：我们的算法应该对于任意符合条件的输入都应用，而不是只适用某些特定的输入。The procedure should be applicable for all problems of the desired form, not just for a particular set of input values.

correctness 和 effectiveness 辨析 ★

correctness 主要将算法应该给出 correct output values，而 effectiveness 则主要指出算法应当是可以被 exactly execute。作业题中有一题是一算法会出现 $1/0$ 的情况，应该判定为缺少 effectiveness.

2. 函数的增长 The Growth of Functions

2.1. 渐进运行时间 Asymptotic Running Time

渐进运行时间(asymptotic running time) is the number of operations used by the algorithm as the input size approaches infinity.

2.2. 记号 Notations

大 O 记号(Big-O notation)：Let $f$ and $g$ be functions from $Z$ (or $R$ ) to $R$ . We say that “ $f(x)$ is $O(g(x))$ ” if there are constants $C$ and $k$ such that $|f(x)| \le C|g(x)|$ whenever $x>k$ .

大 $\Omega$ 记号(Big-Omega notation)：Let $f$ and $g$ be functions from $Z$ (or $R$ ) to $R$ . We say that “ $f(x)$ is $\Omega(g(x))$ ” if there are constants $C$ and $k$ such that $|f(x)|\ge C|g(x)|$ whenever $x>k$ .

大 $\Theta$ 记号(Big-Theta notation)：Let $f$ and $g$ be functions from $Z$ (or $R$ ) to $R$ . We say that “ $f(x)$ is $\Theta(g(x))$ ” if “ $f(x)$ is $O(g(x))$ ” and “ $f(x)$ is $\Omega(g(x))$ ”, i.e., there are constants $C_1$ , $C_2$ , and $k$ such that $0\le C_1 g(x) \le f(x) \le C_2 g(x)$ whenever $x>k$ .

3. 算法的复杂度 Complexity of Algorithms

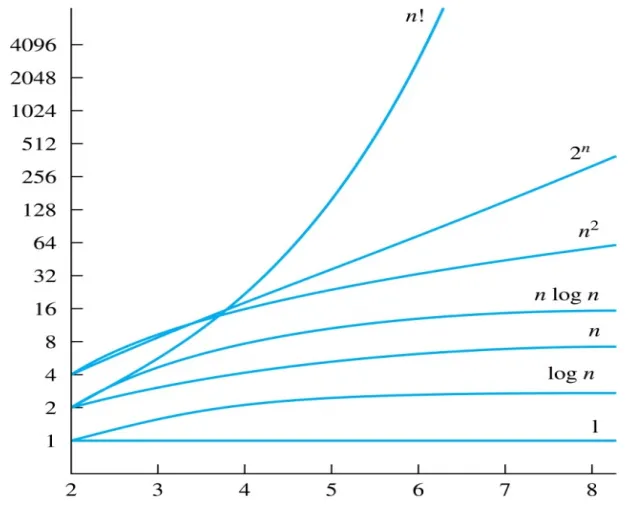
Commonly used Terminology for the Complexity of Algorithms

Complexity	Terminology
$\Theta(1)$	常数复杂度(constant complexity)
$\Theta(\log n)$	对数复杂度(logarithmic complexity)
$\Theta(n)$	线性复杂度(linear complexity)
$\Theta(n \log n)$
$\Theta(n^b)$	多项式复杂度(polynomial complexity)
$\Theta(b^n)$	指数复杂度(exponential complexity) (b>1)
$\Theta(n!)$	阶乘复杂度(factorial complexity)

TABLE OF CONTENTS

1. 算法 Algorithms

1.1. 导论 Introduction

1.2. 算法的性质 Properties of Algorithms

2. 函数的增长 The Growth of Functions

2.1. 渐进运行时间 Asymptotic Running Time

2.2. 记号 Notations

3. 算法的复杂度 Complexity of Algorithms

1. 算法 Algorithms

1.1. 导论 Introduction

1.2. 算法的性质 Properties of Algorithms

2. 函数的增长 The Growth of Functions

2.1. 渐进运行时间 Asymptotic Running Time

2.2. 记号 Notations

3. 算法的复杂度 Complexity of Algorithms

评论