本篇笔记主要介绍了树的基本概念和术语，包括树的定义、性质、不同类型的树（如二叉树和 $m$ 叉树）、树的应用（如二叉搜索树和前缀编码）、树的遍历方法以及生成树的相关内容。通过这些内容的学习，读者将能够理解树在离散数学中的重要性，并掌握如何分析和应用这些树的知识。（由 gpt-4o-mini 生成摘要）

1. 树论术语 Tree Terminologies

树(tree) 是没有简单环的连通无向图。

森林(forest) 是没有简单环的无向图。

有根树(rooted tree)：在树的若干节点中，选择一个特定的节点作为根(root)，这样的树称为有根树，在有根树中我们有如下概念：

• 父亲节点(parent)：对于非根节点 $v$，其父亲节点是唯一的有指向 $v$ 的有向边的节点（以根节点为起点给边定向）。
• 孩子节点(child/children)：若 $u$ 是 $v$ 的父亲，则称 $v$ 是 $u$ 的一个孩子节点。
• 兄弟节点(sibling)：有相同父亲节点的两个节点互称兄弟节点。
• 祖先节点(ancestor)：节点 $v$ 的祖先是从根到 $v$ 的路径上的所有节点。
• 后代节点(descendant)：若 $u$ 是 $v$ 的祖先，则称 $v$ 是 $u$ 的一个后代节点。
• 叶子节点(leaf)：没有孩子节点的节点称为叶子节点。
• 内部节点(internal vertex)：有孩子节点的节点称为内部节点。
• 子树(subtree)：点 $v$ 的子树是指 $v$ 和 $v$ 的所有后代节点组成的子图。

2. 树的性质 Tree Properties

一棵 m-叉树被认为是平衡的当且仅当每个叶子节点的深度不是 $h$ 就是 $h-1$。

3. 二叉树 Binary Tree

m 叉树(m-ary tree)：每个节点的孩子个数都不超过 $m$ 的有根树。

二叉树(binary tree)：每个节点的孩子个数都不超过 $2$ 的有根树。

满二叉树(full binary tree)：每个非叶节点的孩子个数都恰好为 $2$ 的有根树。（即每个节点要么有两个儿子要么没有儿子，叶子结点可以不全在同一深度）

有序二叉树(ordered binary tree)：每个节点都有一个可能的左孩子和右孩子，据此可以定义左子树(left subtree) 和右子树(right subtree)。

节点 $v$ 的深度(level, depth)：根节点到 $v$ 的路径长度。（根节点的深度定义为 $0$。）

树 $T$ 的高度(height)：所有节点的深度最大值。

4. 树的应用 Applications of Trees

4.1. 二叉搜索树 Binary Search Tress

二叉搜索树(binary search tree, BST)：略。

4.2. 前缀编码 Prefix Codes

前缀编码(prefix codes)：是一种编码方式，这样对于每个编码后的 01 串，他们都没有共同的前缀。相当于画出字典树的话所有编码最后都走到了叶子结点上。

用哈夫曼编码(huffman coding) 的方法可以最小化每一字符编码后的平均位长。

4.3. 树的遍历 Tree Travelsal

• 先序遍历(preorder travelsal)
• 中序遍历(inorder travelsal)
• 后序遍历(postorder travelsal)

4.4. 表达式表示法 Expression Notations

• 前缀形式(prefix form)，波兰表达式(Polish notation)
• 中缀形式(infix form)
• 后缀形式(postfix form)，逆波兰表达式(reverse Polish notation)

5. 生成树 Spanning Tree

图 $G$ 的生成树(spanning tree) 是包含 $G$ 中每一个节点的子图。

5.1. 深度优先搜索 & 宽度优先搜索 DFS & BFS

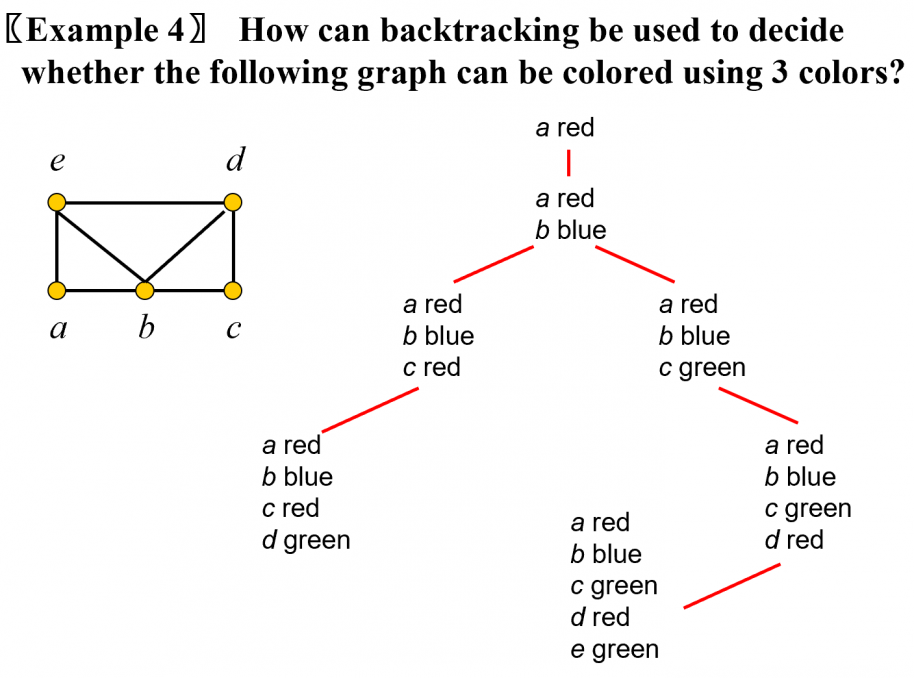
深度优先搜索(depth-first search, DFS) 又叫做回溯(backtracking)。

宽度优先搜索(breadth-first search, BFS)。

可以用 DFS 或 BFS 来解决一些数据规模小的离散问题。

5.2. 最小生成树 Minimum Spanning Trees

• Prim’s algorithm：随便选定一个点作为开始的最小生成树，每次把与最小生成树外的点相连的最小边及其新增点加入最小生成树，直到得到整张图的最小生成树。

• Kruskal’s algorithm：把所有边按照大小从小到大的顺序枚举，如果两端点不在同一个联通块中则将这条边加入最小生成树。