「Petrozavodsk Summer 2020」Parity Sort

2021 年 01 月 21 日

定义一个排列 $P$ 上的操作 $(t,S)$ 为：

有两个空序列 $A$ 和 $B$ ；

枚举 $S_i=1$ 的每个 $i$ ：如果 $P_i$ 是偶数，则将其放到 $A$ 的末尾；否则放到 $B$ 的末尾；

如果 $t=0$ 则令 $C=\overline{AB}$ ，否则令 $C=\overline{BA}$ ；

枚举 $S_i=1$ 的每个 $i$ ：将 $P_i$ 替换为 $C$ 的开头元素，删去 $C$ 的开头元素。

现给定排列 $P$ ，要求使用至多 $30$ 次如上操作，使 $P$ 从小到大排序，注意你不需要最小化操作次数。

$1\le n\le 15000$ 。

题意补充

对于 $P=\{0,4,2,3,6,5,1\}$ 上的操作 $(1,\texttt{1101101})$ ，有示意图如下

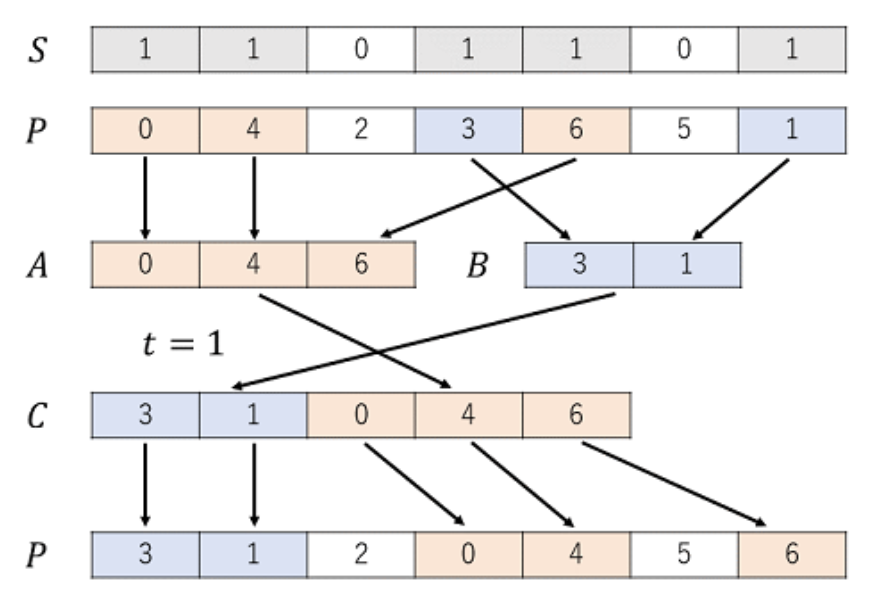
题解

由于 $30=2\left(\left\lfloor\log n\right\rfloor\right)+1$ ，我们考虑 $t=0$ 和 $t=1$ 的操作交错执行。

首先可以确定最后一次操作前，每个数的位置，如 $n=13$ 的时候，最后一次操作前的 $p$ 应为：

0 8 2 10 4 12 6 7 1 9 3 11 5

故对于每个数，我们求出此时期望的位置 $rk$ ，也就是说，现在我们要把每个 $p_i$ ，移动到 $rk_{p_i}$ 的位置上。

考虑从低位到高位，每次把这一位是 $1$ 的数不改变相对顺序地丢到最后面， $\log$ 次后即可完成排序。

先进行一次 $(0,111\ldots 1)$ 操作后，所有偶数都在奇数前面，我们可以认为是两个序列；把偶数中需要放后面的数和奇数中需要放前面的数执行 $t=1$ 操作即可。但 $n$ 时可能两侧的数字个数不同，这时候给偶数序列中多丢一个 $0$ 就好了。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1.5e5 + 9;
int n, m, t, p[N], rk[N];
string s;
vector<int> a, b, c;
vector<pair<bool, string>> ans;
void apply(bool t, const string &s) {
  a.clear(), b.clear();
  for (int i = 0; i < n; i++)
    if (s[i] == '1') (p[i] & 1 ? b : a).push_back(p[i]);
  if (t) swap(a, b);
  c = a, c.insert(c.end(), b.begin(), b.end());
  reverse(c.begin(), c.end());
  for (int i = 0; i < n; i++)
    if (s[i] == '1') p[i] = c.back(), c.pop_back();
  ans.push_back(make_pair(t, s));
}
void solve() {
  int s00 = ((n + 1) / 2 + 1) / 2, s01 = (n + 1) / 4, s10 = s01, s11 = n / 2 - s10;
  assert(s00 + s01 + s10 + s11 == n);
  for (int i = 0; i < s00; i++) rk[i << 1] = i << 1;
  for (int i = 0; i < s10; i++) rk[(i + s00) << 1] = i << 1 | 1;
  for (int i = 0; i < s01; i++) rk[i << 1 | 1] = (i + s00) << 1;
  for (int i = 0; i < s11; i++) rk[(i + s10) << 1 | 1] = (i + s10) << 1 | 1;
  for (int i = 1; i < n; i += 2) rk[i] = n - 1 - rk[i] + (n & 1);
  for (int k = 0; k < 14; k++) {
    apply(0, string(n, '1'));
    s = string(n, '0');
    int t = 0;
    for (int i = 0; i < n; i++)
      if (p[i] % 2 == 0 && (rk[p[i]] >> k) % 2 == 1) s[i] = '1';
    for (int i = 0; i < n; i++)
      if (p[i] % 2 == 1 && (rk[p[i]] >> k) % 2 == 1) s[i] = '1';
    apply(1, s);
  }
  apply(0, string(n, '1'));
  s = string(n, '0');
  for (int i = 0; i < n; i++)
    if (p[i] != i) s[i] = '1';
  apply(1, s);
  for (int i = 0; i < n; i++) assert(p[i] == i);
}
int main() {
#ifdef memset0
  freopen("1.in", "r", stdin);
#endif
  cin.tie(0)->sync_with_stdio(0);
  cin >> n;
  for (int i = 0; i < n; i++) cin >> p[i];
  solve();
  cout << ans.size() << endl;
  for (const auto &it : ans) cout << (it.first ? 1 : 0) << " " << it.second << endl;
}

TABLE OF CONTENTS

题意补充

题解

代码

题意补充

题解

代码

评论